Уравнение Максвелла. Ток смещения

Для стационарных токов проводимости конденсатор является разрывом в цепи, так как силовые линии электрического поля начинаются и заканчиваются на зарядах. Возникает вопрос: каким образом происходит зарядка конденсатора? Если линии напряженности прерываются, а перенос заряда все-таки происходит, значит, между пластинами конденсатора должны существовать токи смещения 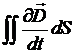. Таким образом, в контуре могут существовать как токи проводимости , так и токи смещения: . 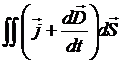Известно, что вокруг проводника с током возникает магнитное поле, индукция которого определяется теоремой о циркуляции:
, или, в общем, 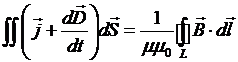(16). Введем величину, определяющую поведение магнитного поля в веществе – напряженность магнитного поля  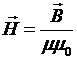    (17), тогда, сделав замену переменных, применим к правой части (16) теорему Стокса: , тогда выражение (16) примет вид 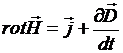(19)
        Выражения (12), (16), (18) и (19) являются фундаментальными уравнениями электродинамики и представляют собой систему уравнений Максвелла:
1) 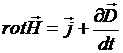 - вихревое магнитное поле может быть создано токами проводимости и токами смещения;
2) 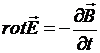 - меняющееся со временем магнитное поле порождает вихревое электрическое поле;
3) - отсутствие магнитных зарядов;
4)  - электростатическая теорема Гаусса;
5)  - связь напряженности электрического поля и вектора смещения (индукции электрического поля)
6) - связь напряженности и индукции магнитного поля