Закон Ома для участка цепи

1.2. Закон Ома для участка цепи с ЭДС
    На практике часто встречается задача, когда требуется определить ток в некоторой ветви при известных ее параметрах и потенциалах ее зажимов.
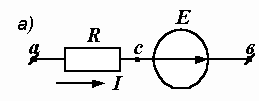
    Пусть в схеме на рис. 1.8, а заданы R, E, ф a, ф b, и требуется определить ток.

Рис. 1.8. Варианты ветви с ЭДС
    Между R и E отметим промежуточную точку с и выразим ее потенциал через потенциалы точек а и b.
    Так как в резисторе ток протекает слева направо, то потенциал точки а выше потенциала точки с на величину падения напряжения в активном сопротивлении:
ф a = ф с + IR.                                                          (1.4)
    Точка b находится на положительном полюсе источника, а с – на отрицательном. Поэтому
ф b = ф с + E.                                                         (1.5)
    Беря разность левых и правых частей выражений (1.4) и (1.5), получим
ф a – ф b = IR – Е,
откуда
.
    Для цепи на рис. 1.8, б после аналогичных рассуждений будем иметь
I = (ф a – ф b – E) G.
    В двух последних формулах ЭДС записывается с плюсом, если ее направление на схеме совпадает с направлением тока, и с минусом – в противоположном случае.