Метод контурных токов

1.3.3. Метод контурных токов
    Для каждого из взаимно независимых контуров назначается так называемый контурный ток, замыкающийся по всем ветвям контура. Направления этих токов произвольны.

Рис. 1.9. Сложная электрическая цепь

    На рис. 1.9 они обозначены дугообразными стрелками, рядом с которыми стоят буквы IK1, IK2, IK3 и IK4. Для выбранных контурных токов записываются уравнения по второму закону Кирхгофа. Контур при этом обходится по направлению контурного тока. Рассмотрим порядок составления уравнения на примере третьего контура. Контурный ток IK3, протекая по сопротивлениям своего контура, создает на них падение напряжения

                 (1.10)

    По сопротивлению R4, являющемуся элементом третьего контура, протекает контурный ток IK2. Создаваемое им падение напряжения IK2R4 вычитается из предыдущего, так как направление тока IK2 в сопротивлении R4 противоположно току IK3. Сопротивление R6 также входит в третий контур. Падение напряжения на нем, создаваемое контурным током IK4, складывается с суммой (1.10), так как направления IK4 и IK3 в R6 одинаковы. В правой части уравнения записывается алгебраическая сумма всех ЭДС контура, в данном случае – единственная ЭДС E4.
    Итак, для третьего контура имеем:

    Аналогично составляются и остальные контурные уравнения:

    После решения последней системы действительные токи ветвей определяются по найденным контурным:

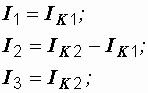
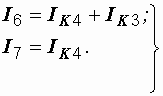                 (1.11)

    Контурные уравнения получаются подстановкой формул (1.11) в уравнения второго закона Кирхгофа (1.7).