Метод эквивалентного генератора

1.5. Метод эквивалентного генератора
    Этот метод основан на сформулированной выше теореме (см. подразд. 1.4) и применяется в тех случаях, когда требуется рассчитать ток в какой-либо одной ветви при нескольких значениях ее параметров (сопротивления и ЭДС) и неизменных параметрах всей остальной цепи.
    Сущность метода заключается в следующем. Вся цепь относительно зажимов интересующей нас ветви представляется как активный двухполюсник, который заменяется эквивалентным генератором, к зажимам которого подключается интересующая нас ветвь. В итоге получается простая неразветвленная цепь, ток в которой определяется по закону Ома.
ЭДС ЕЭ эквивалентного генератора и его внутреннее сопротивление RЭ находятся из режимов холостого хода и короткого замыкания двухполюсника.
    Порядок решения задачи этим методом рассмотрим на конкретном числовом примере.
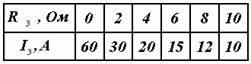
    Пример 1.5. В цепи, показанной на рис. 1.20, а, требуется рассчитать ток I3 при шести различных значениях сопротивления R3 и по результатам расчета построить график зависимости I3(R3).
    Числовые значения параметров цепи: Е1 = 225 В; Е3 = 30 В; R1 = 3 Ом; R2 = 6 Ом.
                          а)                                                                   б)

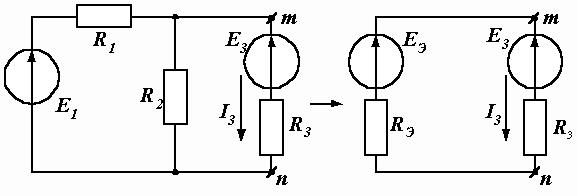
Рис. 1.20. Схема решения задачи
    Р е ш е н и е. а) Расчет режима холостого хода.
    Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 1.21, а). Напряжение между ними, равное UX, находится как падение напряжения на сопротивлении R2:
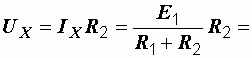150 В;       150 В.
    б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 1.21, б). Ток короткого замыкания 75 А.
    Внутреннее сопротивление эквивалентного генератора
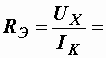2 Ом.

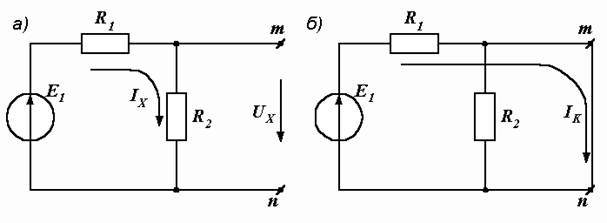
Рис. 1.21. Режимы холостого хода (а) и короткого замыкания (б)
    Величину RЭ можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. 1.21, а мысленно закоротить зажимы ЭДС Е1, то сопротивления R1 и R2 окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно 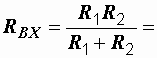2 Ом.
    Ток в полученной неразветвленной цепи (рис. 1.20, б) определяется по закону Ома:
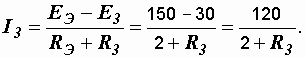                                     (1.13)
    Подставляя в последнюю формулу требуемые значения сопротивления R3, вычисляем ток и строим график (рис. 1.22).

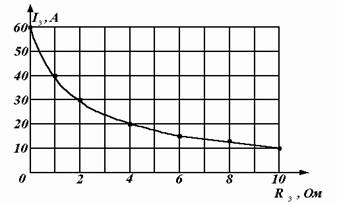Рис. 1.22. Зависимость тока от сопротивления

    Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя ЕЭ и RЭ, а многократно используем лишь одну простую формулу (1.13).