Синусоидальный ток в индуктивности

2.10. Самоиндукция. Индуктивность. Синусоидальный ток в индуктивности
    Если в катушке, изображенной на рис. 2.1, магнитное поле создается собственным током i, то магнитный поток называется потоком самоиндукции и обозначается ФL, а индуцируемая в катушке ЭДС еL – ЭДС самоиндукции. В соответствии с формулой (2.1) она равна
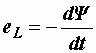,                                                         (2.15)
где – потокосцепление самоиндукции, величина, пропорциональная протекающему по катушке току: = Li.
    Коэффициент пропорциональности L между потокосцеплением и током называется собственной индуктивностью или просто индуктивностью катушки (контура). Она зависит от формы и размеров катушки, а также от магнитной проницаемости сердечника. Ее размерность В x с/А=Ом x с. Эта единица измерения называется генри (Гн).
    Подставляя последнее выражение в (2.15) и полагая L = const, получаем следующую формулу, определяющую ЭДС самоиндукции:
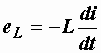.                                                           (2.16)

    Все три стрелки на схеме (i, eL, uL) принято направлять в одну сторону. Раньше мы видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому
.                                                           (2.17)
    Знак минус в правой части формулы (2.16) обусловлен принципом Ленца, определяющим направление индуцированной ЭДС. В рассматриваемом случае он может быть сформулирован следующим образом:
    ЭДС самоиндукции направлена так, что своим действием препятствует причине, вызвавшей ее появление.
    Причина появления ЭДС самоиндукции – изменение тока. Поэтому при возрастании тока она направлена ему навстречу, при уменьшении тока – в одну с ним сторону.
    Препятствуя изменению тока, ЭДС самоиндукции оказывает ему сопротивление, которое называется индуктивным и обозначается хL. В соответствии с формулой (2.16) его величина определяется индуктивностью и скоростью изменения тока, т.е. частотой. Формула, определяющая индуктивное сопротивление, имеет вид:
.
    В цепях постоянного тока такого понятия мы не встречали, так как при постоянных магнитных полях ЭДС самоиндукции не возникает.
    Пусть ток, протекающий по индуктивности, определяется выражением (2.13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно
.
     Это – мгновенное значение напряжения. Его амплитуда равна
.
    Аналогичное выражение получается (после деления на ) и для действующих значений
, откуда ,
где ВL – индуктивная проводимость; .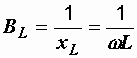
    Запишем соответствующие формулы в символической форме:
.
    Так как , то .
    Отсюда .
    Аналогично для действующих значений:
                                          ,
.                                               (2.18)

  Согласно уравнениям (2.18) получается путем умножения произведения на j, в результате чего вектор оказывается повернутым относительно вектора .

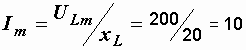    Пример 2.5. Мгновенное значение напряжения на индуктивности определяется выражением uL = 200 sin( t+60°) В. Записать выражение мгновенного значения тока, если L = 63,67 мГн, а частота питающего напряжения f = 50 Гц. Построить векторные диаграммы напряжения и тока.