Цепь переменного тока с емкостью

2.11. Синусоидальный ток в емкости

Система из двух проводящих тел, разделенных диэлектриком, образует конденсатор. Эти проводящие тела называются обкладками. Если к ним подключить источник энергии, то на них будет накапливаться заряд q, пропорциональный напряжению на конденсаторе uC (рис. 2.21):

Image5016.gif (1393 bytes)
Рис. 2.21. Обозначение конденсатора

q = CuC..                                                                               (2.19)
    Коэффициент пропорциональности C между зарядом и напряжением называется емкостью конденсатора. Единица измерения емкости – фарада (Ф). Она имеет следующую размерность: 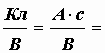. Емкость зависит от формы, размеров конденсатора и от диэлектрической проницаемости диэлектрика между обкладками.
    Пусть напряжение, подаваемое источником на конденсатор, изменяется по закону
uC = UCm sin ( t+ ).                                                     (2.20)
    При его возрастании от нуля до максимального значения конденсатор заряжается, на его обкладки от источника поступает электрический заряд. При уменьшении напряжения от максимума до нуля, заряд стекает с конденсатора, он разряжается. Таким образом, в проводах, соединяющих конденсатор с остальной цепью, постоянно движется электрический заряд, т.е. протекает электрический ток. Вывод о наличии электрического тока мы делаем, совершенно не касаясь вопроса о том, какие процессы происходят между обкладками конденсатора. Величина тока определяется зарядом, прошедшим в единицу времени через поперечное сечение проводника:
.                                                       (2.21)
    Она зависит от емкости и скорости изменения питающего напряжения, т.е. от частоты. От этих же факторов зависит и электрическая проводимость участка цепи с конденсатором. Ее называют емкостной проводимостью и определяют по формуле
BC = C = 2pfC.
    Величина, обратная емкостной проводимости, называется емкостным сопротивлением:
Image5020.gif (1362 bytes) .
    Подставляя в (2.21) приложенное к конденсатору напряжение из (2.20), получаем
                             (2.22)
где Im = CUCm = BcUCm.
    Действующее значение тока
I = CUC = BCUC,
    Отсюда .
    Последние три уравнения представляют разные формы записи закона Ома для конденсатора. Запишем их в символической форме. На основании (2.20) и (2.22):
,
,
или .
    Отсюда .
    Векторная диаграмма, построенная по приведенным выше уравнениям, показана на рис. 2.22.
    Угол наклона каждого вектора к положительному направлению вещественной оси определяется начальными фазами в выражениях (2.20) и (2.22). Так как при определении напряжения мы умножаем на –j, то вектор оказывается повернутым относительно вектора тока на угол 90° в отрицательном направлении, по часовой стрелке. Как отмечалось раньше, направление угла ф на диаграмме показывается от вектора тока к вектору напряжения.

Рис. 2.22. Векторная диаграмма напряжения и тока в емкости
    Пример 2.6. Напряжение на конденсаторе uC = 100sin (1000t –30°). Написать выражение мгновенного значения тока через конденсатор. Каким станет ток, если частота питающего напряжения увеличится вдвое? Емкость конденсатора С = 50 мкФ.
    Р е ш е н и е. Определяем емкостное сопротивление:
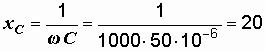Ом.
    Амплитуда тока A.
    Так как , а и , то начальная фаза тока
.
    Таким образом, .
    При возрастании частоты вдвое емкостное сопротивление уменьшается также вдвое: Ом.
    Амплитуда тока при этом увеличивается: A.
    Так как угол сдвига фаз не меняется, то мгновенное значение тока будет равно
А.