Закон Ома в комплексной форме

2.15. Закон Ома в символической форме для произвольной цепи
    Пусть мгновенные значения напряжения и тока на зажимах произвольного пассивного двухполюсника определяются выражениями (2.3). Тогда комплексы их действующих значений соответственно равны
                         ,
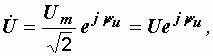
а их отношение определяет комплексное сопротивление двухполюсника

    Величина, обратная комплексному сопротивлению, – комплексная проводимость
.
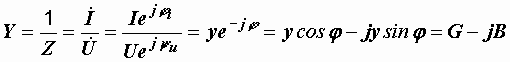    Сопротивления z, R, x и проводимости y, G и B, входящие в два последних выражения, есть не что иное, как эквивалентные параметры двухполюсника, о которых говорилось в подразделе 2.14.
    Пример 2.19. Определить эквивалентные активное и реактивное сопротивления цепи, если мгновенные значения напряжения и тока на ее входных зажимах соответственно равны
В, А.
    Р е ш е н и е.
Ом,
т.е. R = 40 Ом, x = 30 Ом.
    Знак минус перед мнимой частью комплексного сопротивления говорит о том, что суммарное реактивное сопротивление цепи носит емкостный характер. Это видно и из условия задачи. Ток опережает напряжение, его начальная фаза больше.
    Пример 2.20. Определить комплексную проводимость цепи, состоящей из последовательно соединенных активного R и реактивного x сопротивлений.
    Решение.

где , .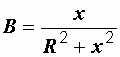