Расчет цепей синусоидального тока

2.16. О расчете цепей синусоидального тока
    Как следует из изложенного теоретического материала и приведенных примеров, при анализе цепей синусоидального тока широко применяются векторные диаграммы и комплексные числа. Сами по себе векторные диаграммы зачастую служат для иллюстрации результатов теоретических исследований и решения задач. Они помогают лучше понять сущность изучаемых процессов и наглядно представить соотношения и связи напряжений и токов на различных участках с параметрами цепи.
    Во многих случаях векторные диаграммы, построенные предварительно по изложенным выше правилам без каких-либо вычислений, являются основой для вывода из них конкретной методики решения данной задачи. Возможны также привязка векторной диаграммы к комплексным осям, выражение векторов комплексными числами и дальнейший расчет в символической форме. Принципиального отличия между методом векторных диаграмм и символическим нет. Как мы видели раньше, за аналитическими действиями с комплексными числами кроются определенные геометрические операции с векторами.
    Следует также помнить, что никакого физического содержания векторы и комплексные числа в себе не несут. Это чисто математические абстракции, необходимые для анализа.
    Символический метод базируется на законах Ома и Кирхгофа, которые в символической форме записываются точно так же, как в цепях постоянного тока. Поэтому все изложенные ранее методы расчета цепей постоянного тока, вытекающие из этих законов, применимы и для расчета в символической форме цепей синусоидального тока.
    Пример 2.21. Рассчитать комплексные сопротивления цепей, изображенных на рис. 2.39, а и б.
    Решение. Сопротивление каждой ветви записываем в символической форме и применяем формулу, известную из теории цепей постоянного тока.
Для схемы, изображенной на рис. 2.39, а:
Ом, Ом,

    Смысл полученного результата заключается в том, что рассматриваемая параллельная цепь может быть заменена эквивалентной последовательной с активным сопротивлением 19,2 Ом и индуктивным 14,4 Ом.
    Для схемы на рис. 2.39, б:
Ом.
    Пример 2.22. Рассчитать цепь, приведенную на рис. 2.40.
    Р е ш е н и е. Находим комплексные сопротивления участков:
Ом,
Ом,
Ом
Ом
    Определяем комплексные токи ветвей:
А,

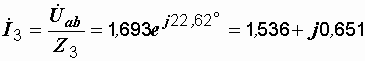А,
А.
    Численные значения токов:
А, А, А.
    Для проверки правильности расчета используем первый закон Кирхгофа в символической форме .
    Смотрим: А.
    В пределах точности расчета закон выполняется.

Рис. 2.39. Схемы к примерам 2.15–2.17