Получение синусоидальной ЭДС
2.2. Получение синусоидальной ЭДС. Характеристики синусоидальных величин. Обозначения в цепях переменного тока
Пусть в однородном магнитном поле, например, между полюсами плоского магнита, под углом 
к горизонтальной плоскости расположена плоская катушка, выполненная в виде прямоугольной рамки, по периметру которой намотано w витков (рис. 2.2). Площадь сечения рамки – S, магнитная индукция – В.
Рис. 2.2. Получение синусоидальной ЭДС
Заставим эту катушку вращаться против часовой стрелки с угловой скоростью w. Если обозначить время полного оборота катушки через Т, то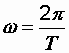 
, рад/с. За некоторый промежуток времени t рамка повернется на угол w t. Площадь проекции рамки в этом положении 
. Рамка и ее проекция на горизонтальную плоскую поверхность пронизываются одним и тем же числом силовых линий магнитной индукции, поэтому обусловленный ими магнитный поток равен
.
При вращении катушки число силовых линий, охватываемых ее витками, все время меняется.
Например, при горизонтальном положении рамки это число максимально, при вертикальном – равно нулю. Другими словами, меняется магнитный поток, пронизывающий катушку, в результате чего в ней в соответствии с уравнением (2.2) наводится ЭДС:
.
Поясним величины, входящие в последнее выражение. Еm – максимальное значение или амплитуда ЭДС. Аргумент синусоидальной функции w t +
называется фазой. Угол 
, определяющий начальное положение рамки и равный фазе в начальный момент времени (при t = 0), – начальная фаза. Фаза с течением времени (при вращении катушки) постоянно меняется. Скорость изменения фазы 
называется угловой или циклической частотой. Время одного цикла изменения фазы (время одного оборота рамки) называется периодом и обозначается T. Количество полных изменений синусоидальной ЭДС в секунду определяет частоту f , измеряемую в герцах (Гц). Один герц соответствует одному полному колебанию в секунду. Связь между частотой и периодом выражается формулой f = 1/T. При частоте 50 Гц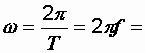 
314 c-1.
Графическое изображение синусоидальной функции времени в электротехнике называют волновой диаграммой. При ее построении на горизонтальной оси откладывается время t или пропорциональный ему угол 
t. При нулевой начальной фазе кривая выходит из начала координат и через каждые четверть периода принимает максимальные значения и переходит через ноль. График такой функции построен по уравнению е = Еm sin
t на рис. 2.3, а.
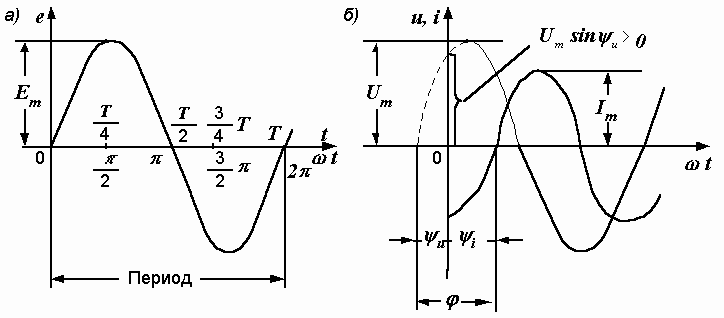
Рис. 2.3. Волновые диаграммы
При ненулевых начальных фазах диаграммы имеют несколько иной вид. Пусть напряжение и ток на некотором участке цепи определяются выражениями:
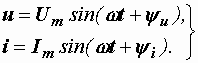(2.3)
Для определенности положим 
u > 0, а 
< 0. Сначала построим волновую диаграмму напряжения. При t = 0 u = Umsin
u. При положительном 
u эта величина положительна, и синусоида отсекает на вертикальной оси отрезок выше начала координат (рис. 2.3, б). Начало синусоиды и все ее точки оказываются сдвинутыми влево на величину 
u. Кривая тока, имея отрицательную начальную фазу, смещается вправо. Если начальные фазы двух синусоидальных функций, изменяющихся с одинаковой частотой, различны, то говорят, что они не совпадают по фазе. Отрезок на горизонтальной оси, разделяющий начала синусоидальных кривых (угол ф на рис. 2.3, б), определяет угол сдвига фаз. Он равен разности их начальных фаз:
ф = 
u – 
i. (2.4)
В случае напряжения и тока вычисление производится именно в таком порядке: начальная фаза напряжения минус начальная фаза тока.
Если 
u > 
i и угол ф положителен, то говорят, что напряжение опережает по фазе ток, или ток отстает по фазе от напряжения. На волновой диаграмме в этом случае кривая напряжения проходит через ноль и максимальные значения раньше тока; изменения тока отстают от соответствующих изменений напряжения. Мера отставания – угол ф.
Остановимся еще на двух моментах. В цепях синусоидального тока мы будем встречаться как с переменными, так и с постоянными величинами. Для тех и других применяются различные обозначения. Переменные величины – функции времени – будем обозначать маленькими (строчными) буквами u, i, e, а постоянные – большими (прописными) U, I, Е.
Второй момент касается указания направления тока или напряжения. При постоянном токе его направление связано с движением положительно заряженных частиц. В случае переменного тока его стрелка на схеме показывает у с л о в н о в ы б р а н н о е положительное направление. Если в какой-то момент времени ток направлен по стрелке, он считается положительным, в противном случае он отрицателен.