Фильтр симметричных составляющих
11. Фильтры симметричных составляющих
Фильтрами симметричных составляющих называются технические устройства или схемы, служащие для выделения соответствующих составляющих токов или напряжений из несимметричной трёхфазной системы векторов.
Напряжения и токи, выделяемые фильтрами симметричных составляющих, используются на практике в качестве входных величин для релейной защиты энергетических установок (генераторов, трансформаторов, линий электропередачи) от несимметричных режимов, возникающих в результате коротких замыканий, или для соответствующей сигнализации о несимметричном режиме.
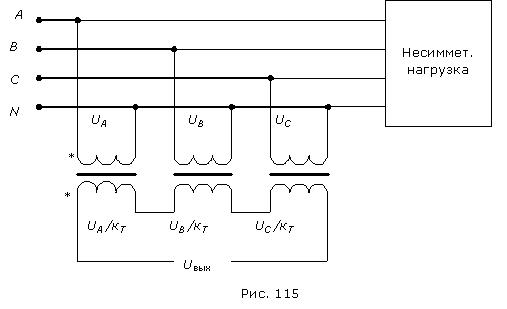
На рис. 115 представлена схема фильтра напряжения нулевой последовательности. Схема фильтра состоит из 3-х одинаковых трансформаторов с коэффициентом трансформации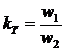 
. Первичные обмотки трансформаторов включены на фазные напряжения 
по схеме звезды с нулевой точкой, а вторичные – в открытый треугольник.
Напряжение на выходе фильтра равно векторной сумме вторичных напряжений трансформаторов:
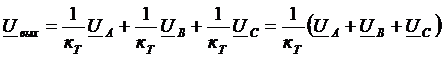
Учитывая, что 
, получим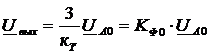 
, где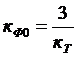 
- коэффициент фильтра.
Фильтр напряжений обратной последовательности реализуется схемой рис. 116 при следующих соотношениях между параметрами элементов: 
, 
, 
.
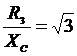
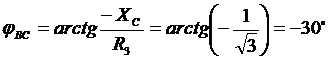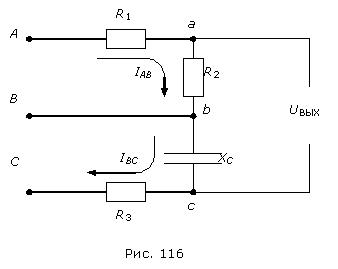
Напряжение на отдельных участках схемы с учетом заданных соотношений между параметрами элементов:
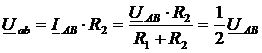
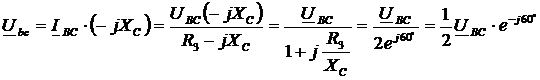
Выходное напряжение фильтра:
Преобразуем формулу для напряжения обратной последовательности путем добавления и вычитания члена aUB:
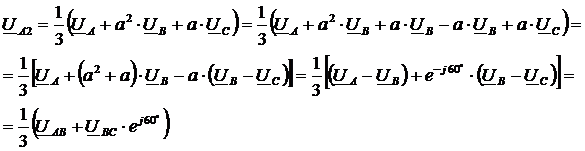
Сравнивая полученное уравнение с предыдущим, найдём:
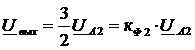, где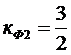 
- коэффициент фильтра.
Векторная диаграмма напряжений фильтра показана на рис. 117а – для симметричной системы напряжений обратной последовательности, и на рис. 117б – для симметричной системы напряжений прямой последовательности.
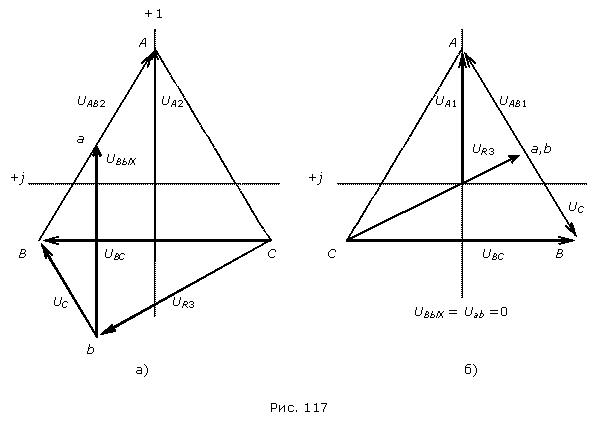
Так как системы прямой и обратной последовательностей отличаются только порядком следования фаз, то из этого следует, что фильтр, выделяющий напряжение одной из этих последовательностей превращается в аналогичный фильтр для выделения напряжений другой последовательности путем перестановки любых двух фаз местами.