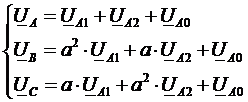Метод симметричных составляющих
9.Теоретические основы метода симметричных составляющих
Метод симметричных составляющих применяется для расчета трехфазных цепей в несимметричных режимах. Несимметричные режимы в энергосистеме возникают при различных видах коротких замыканий. Расчет токов коротких замыканий – важная инженерная задача в электроэнергетике, которая решается методом симметричных составляющих.
Математически любая несимметричная трехфазная система векторных величин (напряжений, токов и др.) может быть представлена в виде суммы (заменена суммой) из трех симметричных трехфазных систем, а именно:
а) системы прямой последовательности с прямым порядком следования фаз A→B→C→A;
б) системы обратной последовательности с обратным порядком следования фаз A→C→B→A;
в) системы нулевой последовательности, которая состоит из трех равных векторов, совпадающих по фазе.
Отдельные симметричные системы векторов, на которые раскладывается несимметричная система, называются симметричными составляющими. Вектора симметричных составляющих индексируются цифрами:
1 - для прямой последовательности,
2 - для обратной последовательности и
0 – для нулевой последовательности.
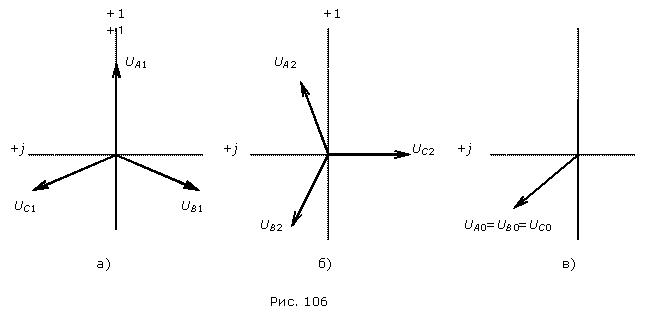
На рис. 1 представлены симметричные составляющие некоторой несимметричной трехфазной системы напряжений UA,UB,UC.
В методе симметричных составляющих для упрощения формы записи уравнений пользуются коэффициентом 
(поворотный множитель), умножением на который поворачивают вектор на угол в 120 без изменения его модуля. Свойства поворотного множителя: 
, 
, 
, 
.
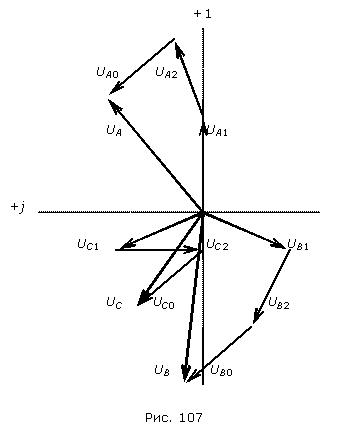
Вектора исходной несимметричной системы определяются по принципу наложения как геометрические суммы соответствующих векторов симметричных составляющих:
Геометрическое сложение векторов симметричных составляющих согласно этим уравнениям показано на рис. 107.
Используя поворотный множитель “a” и “a2”, выразим все слагаемые правой части уравнений через симметричные составляющие фазы А:
|
|
Умножим все члены уравнения (2) на “a”, а все члены уравнения (3) на “a2”, сложим все три уравнения почленно и получим:
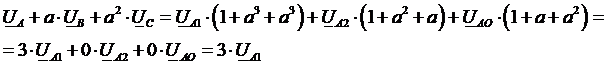Из полученного уравнения следует формула для выделения симметричной составляющей прямой последовательности из несимметричной системы векторов:
.
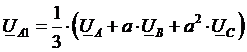Умножим все члены уравнения (2) на “a2”, а все члены уравнения (3) на “a”, сложим все три уравнения почленно и получим:
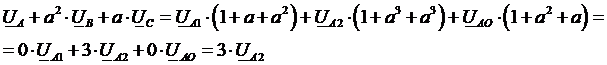Из полученного уравнения следует формула для выделения симметричной составляющей обратной последовательности из несимметричной системы векторов:
.
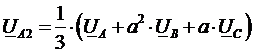Сложим все три уравнения (1), (2) и (3) почленно и получим:
.
Из полученного уравнения следует формула для выделения симметричной составляющей нулевой последовательности из несимметричной системы вектор:
.
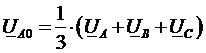Полученные формулы применяются на практике для разложения несимметричных трехфазных систем векторов на симметричные составляющие.